Hướng dẫn cách tính diện tích hình thang dễ hiểu nhất

 

Việc tính diện tích hình thang không chỉ quan trọng trong toán học mà còn được ứng dụng rộng rãi trong thực tế. Qua bài viết này, Pico sẽ cùng bạn tìm hiểu chi tiết nhé!

 

Hình thang là gì?

 

Chắc hẳn bạn đã từng nhìn thấy một chiếc bánh pizza bị cắt không đều. Miếng pizza đó có thể trông giống một hình thang. Vậy chính xác thì hình thang là gì? Hình thang là một hình phẳng có bốn cạnh, nhưng có điểm đặc biệt là hai cạnh đối diện của nó song song với nhau. Bạn có thể tưởng tượng nó giống một chiếc thang để leo trèo, phần trên thường hẹp hơn phần dưới. Đó chính là lý do tại sao nó được gọi là hình thang.

Trong hình thang, hai cạnh song song được gọi là đáy. Đáy dài hơn thường được gọi là đáy lớn, còn đáy ngắn hơn là đáy nhỏ. Hai cạnh còn lại không song song, chúng được gọi là cạnh bên. Hình thang có thể có nhiều dạng khác nhau, ví dụ như hình thang cân (hai cạnh bên bằng nhau) hay hình thang vuông (một cạnh bên thẳng đứng).

Hiểu về hình thang rất hữu ích, vì chúng ta thường gặp nó trong cuộc sống hàng ngày, từ hình dạng của mái nhà cho đến thiết kế của nhiều đồ vật xung quanh ta.

 

 

Công thức tính diện tích hình thang

Tính diện tích hình thang là kỹ năng quan trọng trong hình học và ứng dụng thực tế. Mặc dù có một công thức chung, nhưng tùy trường hợp, ta có thể áp dụng công thức riêng để tính nhanh và hiệu quả hơn. Cụ thể như sau:

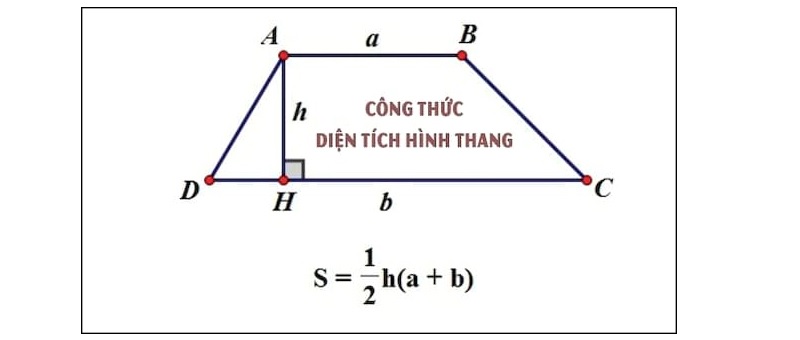
Công thức chung

Công thức chung áp dụng cho mọi loại hình thang. Nó dựa trên độ dài hai đáy và chiều cao. Công thức này đơn giản và dễ nhớ. 

S = h x ((a + b)/2)

Trong công thức này:

S là diện tích của hình thang

h là khoảng cách ngắn nhất từ một đỉnh đến cạnh đáy đối diện, tạo thành góc vuông với đáy

a và b đại diện cho độ dài của hai cạnh song song, thường được gọi là đáy lớn và đáy nhỏ

Công thức tính hình thang cân

Hình thang cân là loại hình thang đặc biệt. Nó có hai cạnh bên bằng nhau. Hình dạng này thường gặp trong kiến trúc và thiết kế. Để tính diện tích hình thang cân, bạn có thể áp dụng công thức chung hoặc chia nhỏ hình ra để tính và cộng tổng lại như bình thường:

S = h x ((a + b)/2)

Công thức tính hình thang vuông

Hình thang vuông là hình thang có một cạnh bên vuông góc với đáy. Nó thường xuất hiện trong các bài toán thực tế. Công thức tính diện tích hình thang vuông như sau:

S = h x ((a + b)/2)

Áp dụng công thức này, ta chỉ cần biết độ dài hai đáy và cạnh vuông góc. Nó giúp tính toán nhanh chóng và chính xác.

 

 

Hướng dẫn cách áp dụng công thức tính diện tích hình thang trong bài toán

Khi tính diện tích hình thang, ta có thể áp dụng các bước sau:

Tính diện tích khi biết a, b và h

Trong đó:

a: độ dài cạnh đáy trên

b: độ dài cạnh đáy dưới

h: chiều cao (vuông góc với đáy)

Bước 1: Tính tổng chiều dài hai đáy

Cộng độ dài hai cạnh đáy song song (a và b).

Ví dụ: a = 8cm, b = 12cm. Tổng: 8 + 12 = 20cm.

Bước 2: Xác định chiều cao h

Đo hoặc tính h từ dữ kiện cho sẵn. Lưu ý: h không phải là cạnh bên, trừ trường hợp hình thang vuông.

Bước 3: Nhân tổng hai đáy với chiều cao

Thực hiện (a + b) × h.

Ví dụ: (8 + 12) × 6 = 120cm²

Bước 4: Chia kết quả cho 2

S = [(a + b) × h] ÷ 2

Ví dụ: S = 120 ÷ 2 = 60cm²

Tính diện tích hình thang vuông

Với hình thang vuông bạn vẫn có thể áp dụng công thức trên, nhưng cạnh bên vuông góc với đáy chính là chiều cao.

Tính diện tích hình thang cân khi biết 4 cạnh

Cách này chỉ áp dụng được cho hình thang cân. Đầu tiên, bạn hãy vẽ hai đường thẳng mới. Mỗi đường xuất phát từ một đỉnh của cạnh song song ngắn hơn, đi xuống vuông góc với cạnh song song dài hơn. Kết quả là hình thang được chia thành ba phần: một hình chữ nhật ở giữa và hai tam giác vuông ở hai bên. Hai tam giác này có đường cao bằng nhau. Cách chia này giúp đơn giản hóa việc tính toán diện tích.

Bước 1: Chia hình thành 2 tam giác vuông và 1 hình chữ nhật

Bước 2: Tính cạnh đáy tam giác

X = (b - a) ÷ 2

Ví dụ: a = 6cm, b = 14cm. X = (14 - 6) ÷ 2 = 4cm

Bước 3: Tìm chiều cao bằng định lý Pytago

c² = a² + b², với c là cạnh huyền (cạnh bên hình thang)

Ví dụ: Cạnh bên = 5cm, X = 4cm

h² = 5² - 4² = 25 - 16 = 9

h = 3cm

Bước 4: Áp dụng công thức diện tích hình thang

S = [(a + b) × h] ÷ 2

Ví dụ: S = [(6 + 14) × 3] ÷ 2 = 30cm²

 

Bài tập áp dụng công thức tính diện tích hình thang, hình thang vuông

 

Sau khi đã điểm qua các dạng toán thường gặp, bạn có thể thử sức với các bài tập sau:

Bài 1: Một hình thang có hai đáy dài 8cm và 14cm, chiều cao 6cm. Tính diện tích hình thang này.

Giải: S = h × ((a + b)/2) = 6 × ((8 + 14)/2) = 66 (cm²)

Bài 2: Khu vườn hình thang có đáy lớn 30m, đáy nhỏ 25m. Chủ vườn mở rộng đáy lớn thêm 4m, đáy nhỏ thêm 2m, diện tích tăng 45m². Tính diện tích ban đầu của khu vườn.

Giải:

Chiều cao sau khi mở rộng: h = (S × 2) : (Δa + Δb) = (45 × 2) : (4 + 2) = 15m

Diện tích ban đầu: S = 15 × (30 + 25)/2 = 412,5m²

Bài 3: Hình thang vuông có khoảng cách giữa hai đáy là 18cm. Đáy nhỏ bằng 2/5 đáy lớn. Diện tích hình là 180cm². Tính độ dài hai đáy.

Giải:

Tổng hai đáy: (180 × 2)/18 = 20cm

Gọi đáy nhỏ là x, đáy lớn là y:

x = 2/5y

x + y = 20

=> x ≈ 5,71cm, y ≈ 14,29cm

Bài 4: Hình thang ABCD vuông tại A, có AB = 10cm, CD = 16cm, AD = 9cm. Tính diện tích ABCD.

Giải: S = (AB + CD) × AD/2 = (10 + 16) × 9/2 = 117cm²

Các câu hỏi thường gặp khi tính diện tích hình thang

Khi tính diện tích hình thang, đôi khi bạn sẽ gặp phải những thắc mắc và sai lầm phổ biến. Để giúp bạn hạn chế điều này, Pico đã tổng hợp và giải đáp chi tiết các câu hỏi phổ biến dưới đây:

Công thức S = 1/2 × (b1 + b2) × h có áp dụng được cho mọi hình thang?

Đúng vậy. Công thức này áp dụng cho tất cả các loại hình thang, bao gồm hình thang thường, cân và vuông, miễn là ta biết độ dài hai đáy và chiều cao.

Khi chỉ biết độ dài các cạnh, thì tính diện tích hình thang như thế nào?

Trong trường hợp này, có thể sử dụng định lý Heron để tính diện tích các tam giác tạo thành hình thang (nếu chia được), hoặc áp dụng phương pháp tích phân cho các trường hợp phức tạp hơn.

Cách xác định chính xác chiều cao hình thang?

Chiều cao hình thang là đoạn thẳng vuông góc nối hai đáy. Lưu ý không đo theo đường chéo hay dọc cạnh bên, trừ khi đó là hình thang vuông.

Công thức tính diện tích chung có áp dụng được cho hình thang không đều không?

Chắc chắn rồi. Miễn là xác định được chính xác hai đáy và chiều cao, công thức này áp dụng cho mọi hình thang, đều hay không đều.

Các bước tính diện tích hình thang chính xác nhất:

Bước 1: Xác định độ dài hai đáy (a và b)

Bước 2: Đo chiều cao (h)

Bước 3: Áp dụng công thức: S = (a + b)/2 × h

Bước 4: Thay số vào công thức

Bước 5: Thực hiện phép tính theo thứ tự ưu tiên để có kết quả chính xác

 

 

Việc nắm vững cách tính diện tích hình thang không chỉ giúp bạn đạt điểm cao trong các bài kiểm tra, mà còn hữu ích trong nhiều lĩnh vực như kiến trúc, xây dựng, và thiết kế. Vì vậy, nếu bạn thực hành thường xuyên với các bài tập đa dạng. Không chỉ giúp bạn củng cố kiến thức mà còn giúp bạn phát triển kỹ năng giải toán của mình. Với sự kiên nhẫn và tư duy logic, bạn sẽ dần trở nên thành thạo trong việc tính toán diện tích hình thang các hình học phẳng khác.